Математика 5 класс Прямоугольный параллелепипед Объем

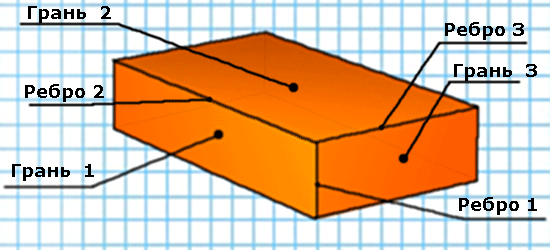
На рисунке изображен прямоугольный параллелепипед. В жизни мы сталкиваемся с такой формой в виде коробка спичек, коробки из-под обуви, кирпича и т.д.
        Прямоугольники, составляющие поверхность параллелепипеда, называются гранями. У параллелепипеда их 6, причем грани расположенные напротив друг друга равны. У параллелепипеда есть 12 ребер, они также являются сторонами граней. Точки схождения ребер называются вершинами параллелепипеда. Площадь грани 1 изображенной на рисунке равна произведению первого и второго ребра.
        Площадь всей поверхности параллелепипеда равна сумме площадей граней 1, 2 и 3 умноженной на 2.

         Прямоугольный параллелепипед определяется тремя измерениями.
        Высота (обозначим буквой h) равна длине ребра № 1.
        Длина (обозначим буквой m) равна длине ребра № 2.
        Ширина (обозначим буквой n) равна длине ребра № 3.
        Если площадь всей поверхности параллелепипеда обозначить буквой S, то формула ее нахождения будет выглядеть так:
        S = (h • m + h • n + n • m) • 2

         Кубом называют прямоугольный параллелепипед, у которого все измерения равны. Поверхность куба составляет 6 равных квадратов.
        Если длину ребра куба обозначить буквой n, то S = n² • 6
        Прямоугольный параллелепипед обладает еще одним измерением, которое называется объем (обозначим буквой V) .
         V = h • m • n

         Величина объем показывает, какую часть пространства занимает объект. В быту объем чаще всего используется для измерения жидкостей, и самая распространенная единица измерения объема является литр = 1 дм³.
        Так же для измерения объема используются м³, мм³, см³, км³.

         Куб с размерами 1 см будет обладать объемом 1 см³.
         V = 1 см • 1 см • 1 см = 1 см³.
        Два таких куба вместе займут вдвое больший объем 2 см³, то есть объем объекта это сумма объемов фигур, из которых состоит объект.